摘要： 近些年来,对于静态图的研究越来越全面、深入，已经形成了完善的理论体系。但是，如果考虑到生活中的一些应用问题，如社交网络中不断变化的关系等，使用静态图表示此类时刻都在变化的关系似乎显得有些乏力。而历史图可以用以表示动态变化。PageRank算法是用于衡量网页重要程度的算法，而网络中不断有网站新建或删除，这样的网络用历史图来表示显得相当贴切，因此我们考虑在历史图上利用CSR(Compressed Sparse Row)结构实现PageRank,使得程序能够给出在几个目标时间的各网站的评分，进而能够提供网站评分的变化情况，给出网站影响力趋势的预测。在Wekipedia提供的网页互相连接的Hyperlink networks数据集上将其性能与在链表上实现PageRank算法作比较，结果显示其性能大大优于使用链表结构，并且随着数据规模和目标时间规模的增大，其优势将会越来越明显。

关键词： PageRank；CSR(Compressed Sparse Row)结构；历史图 

1 引言

1.1 课题背景及研究的目的和意义

在这个时代，大数据是信息化发展到一定阶段的产物。大数据不仅仅是数量上的大，在其背后隐藏着各个行业、领域错综复杂的关系，而这样的关系往往蕴含着商业价值与科研价值[1]。“图”是用来表示关系的一种很好的数据结构，它能够有效且直观地描述现实生活中各个事物之间的复杂关系以及各个事物本身所具有的一些性质。在现实生活中所存在的对象可以抽象为图中的顶点，对象和对象之间的某种或者多种关系可以抽象为顶点与顶点之间的单边或者多边关系。例如在社交网络中，用户与用户之间的好友关系等。

对于传统的图数据来说，它是静态的，只能表示一个单一时刻的数据。但是在真实世界中，对于每时每刻都在变化的生命体及其组成来说，静态图注定无法表示，Przytycka等人认为在未来的工作中从静态网络分析提升到动态网络分析是必不可少的[2]。同理，面对随时随地都在变化的互联网，每时每刻都有页面的不断加入和退出。因此我们需要一个更好的结构来表示该类情况。

1.2 国内外在该研究方向的现状

传统的PageRank 推荐算法需要全图迭代到收敛，因此其时间复杂度非常高，严重影响了推荐的效率。曹军深入分析了PageRank的关键技术，并对其存在的商业问题进行了思考[3]。为了减少算法的耗时，常家伟等人[4]在PageRank算法的迭代过程中加入可控制迭代次数的参数b和一个用于修剪结果向量的阈值α。然后针对主题相关性的问题中，使用了归一化的邻接矩阵的特征值与特征向量来评估节点之间的距离，从而产生最终的推荐列表，而列表中的对象主题相关性则会较高些。对于APP搜索来说，虽然按照关键词搜索出来的应用主题相关性比较高，但是质量参差不齐。因此李春生等人[5]在PageRank算法基础上引入保持时间因子，使用户保存时间越短的 APP 逐渐悬沉下去，保存时间长的 APP 能快速浮上来。在Francisco Pedroche等人[6]的研究中，PageRank被认为是马尔科夫链（1阶）的静止状态，它利用先前状态的知识来转换系统的状态。他们利用“个性化向量”来让PageRank可以偏向某个节点。而且他们将PageRank和多路复用网络结合起来，定义了Multiplex PageRank。

对于传统的静态图完善的理论体系结构来说，历史图仍在发展中。如果时间回退3-5年，鲜有相关论文产出。近几年，越来越多的关注被集中在历史图相关方面的研究。

在文献[7]中，历史图被描述为一系列的静态图序列。由于面向大规模动态图的可达查询研究较少，且尚存在所以压缩困难以及图结构待优化等问题，丁琳琳等人[8]提出了一种支持大规模数据的基于改进哈夫曼编码的可达查询处理方法。该方法首先对预处理图进行结构上的两次压缩，得到双压缩图；其次，基于双压缩图提出一种前缀label索引，该索引能够有效表达节点间的可达关系。最后，提出双压缩图的演进和可达查询处理及优化算法。面向结构变化的动态图匹配问题最早在 2009年由 Wang 和 Chen 提出 , 他们构建邻节点树(NNT)[9]并依此对匹配候选集进行过滤,从而有效减少假阳性匹配结果的产生。 这之后的代表性算法包括IncIsoMatch [10]、SJ-Tree[11]等,它们对子图匹配的执行效率进一步提升提供了不同看法。文献[12]指出：给定一个网络图，计算给定两点之间距离是一个重要的问题。文献介绍了最先进的基于空间相干和基于顶点重要性的方法的综合比较。并使用具有多达两千万个顶点的各种真实道路网络，分别计算了两种技术的预处理时间，空间消耗和查询效率，以此来评估两种技术。

2 PageRank算法

这个简化的排名函数有个小问题。考虑存在只有链入而无链出的节点，那么，在迭代时，这个循环会不断积累权重，而从来不发出权重。对于这样没有出度的网页，设置其对所有网页都有出度。

PageRank迭代计算过程可以表示为算法一

算法1 PageRank算法

输入： Graph G

输出： PageRank Value

1.Initialize:float array PR[]

2.for i=1 up to max_interation do

3. change = 0

4. for node ∈ G.nodes() do

5. PR(node) = ∑_(v∈G.nodes)?(PR(v))/Nv

6. PR(node) += (1-c)/N

7. change += |〖PR〗_old-〖PR〗_new| /*累计该轮与上轮差值*/

8. end for

9. if change < threshold then

10. break

11. end if

12. end for

然而PageRank却忽视了主题性和相关性。例如“苹果”一次对于不同主题就蕴含不同的意思。因此就产生了个性化的PageRank[14]与主题敏感的PageRank[15]来弥补这些问题。如果将PageRank和IF-TDF结合起来[16]能够基于文档内容与用户查询的相似性对文档进行排名。同时，PageRank也可以应用到电力系统[17]和军事通信系统中 [18] 。

3 历史图

历史图数据，又可以称为临时图数据(temporal graph)、动态图数据(dynamic graph)。其顶点可表示某个实体对象，例如网页、通信双方等。其边可表示为对象的关系。图的边或者点上存在时间戳，表示边或者点出现或消失的时间。

历史图结构会随时间的变化而变化，其动态性主要表现为点和边的不确定性。

历史图数据由诸多个Δ构成，每个Δ可以看做一个四元组(v1,v2,operation,timestamp)，分别表示节点1、节点2、操作类型(增\减)和时间戳，一下算法用到的四元组数据就是如此结构。

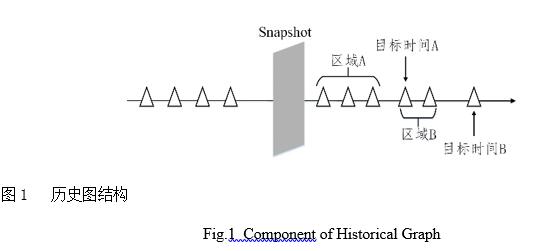
在做历史图相关的计算时，为了避免目标时间距离开始时间过长，我们在线下保存一个整体中部的快照(如图1)，用以表示该时刻的图结构,如果查询时间大于snapshot的时间，那么我们直接读取snapshot的内容即可获得整个时间线半程时的状态。

4 CSR结构

4.1 结构介绍

CSR结构是一种用两个数组表示图数据的数据结构。一个数组（点数组）记录每个点的邻居在另一个数组（边数组）中的位置，边数组就用于存放邻居的编号。如此就可以根据两个数组中的内容还原图中的所有数据。

4.2 结构特点与优势

在空间方面，链表的每个元素包含两个部分，一个部分是存储的数据，另一个部分是指向下一个结点地址的指针，因此用于表示图的时候需要多占用m个指针所需要的空间(m表示边的数目)。而使用CSR结构只需要m+n个int型的空间即可表示同样的图(n表示点的数目)。因此，CSR结构更加省空间。

在时间方面，由于数组的元素在内存空间中是连续存放，而链表存放的空间可以是连续的，也可以是不连续的，因此在遍历数据获取图信息的时候，CSR结构会比链表更快。同时，在处理边的删除操作时，链表需要进行查找、删除、重新指向的操作，比较费时。

5 使用CSR结构实现PageRank

5.1 LinkedList Method

使用最直观的链表维护一个图，对每个delta操作，如果是加边，则到对应的点指向的链表处加上新邻居节点，如果是减边，则在该点的邻居链表中找到对应邻居，删除节点后连接两端。在遇到需要计算PageRank的时间点时，根据当前的图，可以获取所需要的所有信息（节点数目、终止点数目、节点邻居等），然后调用PageRank函数进行计算。

在算法2-1中，首先获取历史图的四元组v(Line2~3)，对于增/减操作进行不同的处理(Line7~11)，如果碰到目标时间则将目标时间的所有操作完成后进行计算PageRank值的操作(3~6)

算法2-1 链表方法

输入：Historical graph data v[4],target time array t[]

输出： PageRank Value in every target time

1. while True do

2. reload v /*读取四元组数据*/

3. node1,node2,ope,time←v[0],v[1],v[2],v[3]

4. if time is one of target times then

5. calPR() /*计算PageRank值*/

6. end if

7. if ope=1 then

8. addNode(node1,node2) /*添边*/

9. else

10. deleteNode(node1,node2) /*减边*/

11. end if

12.end while

5.2 Serial Method

对于CSR结构，最直观的想法是按照时间顺序进行计算。如图2所示，在snapshot处存在一个CSR结构来保存快照（CSR-A，如图2-1），同时将区域A的所有delta按照入射节点排序后生成另一个CSR结构（CSR-B，如图2-2）。相比CSR-A，CSR-B中还存储的增减操作。计算PageRank时，对于点A，从CSR-A中获取邻居（B、C、D），计算PageRank。然后访问CSR-B，补充区域A的操作带来的改变，如果CSR-B中B指向A的边被删除，就说明之前我们多累加了一个值，那么这时候减去即可。以此类推其他点。

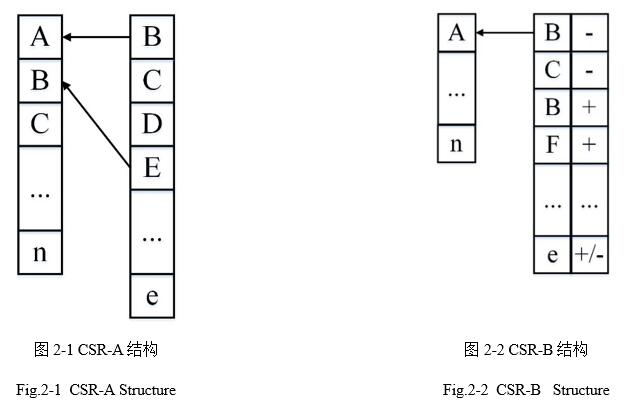
在算法3-1中首先判断查询时间是否集中在时间轴后半部分，是则利用是先处理好的数据生成CSR-A(Line2~5)。之后不断将v添加到ope_array中(Line14)。如果time是目标时间则将ope_array按被指向节点(node2)进行排序，然后生成CSR-B。之后即可根据CSR-A和CSR-B进行PageRank的计算。

算法3-1 线性法PageRank

输入：Historical graph data v[4],half historical graph file h_hg_file,target time array t[]

输出： PageRank Value in every target time

1. initialize:int array ope_array[][4] /*四元组载体*/

2. if first target time >= half_time then

3. h_hg_file.rdbuf()

4. create CSR-A

5. end if

6. while True do

7. reload v

8. node1,node2,ope,time←v[0],v[1],v[2],v[3]

9. if time is one of target time then

10. sort(ope_array) by node2

11. create CSR-B

12. calPR(CSR-A,CSR-B)

13. end if

14. ope_array.append(v)

15. end while

在算法3-2中按照与算法2-2一样的方法初始化PR[](Line1)，之后开始迭代，对于每个点，收集其在CSR-A中的邻居，对PageRank值进行累加。再根据该点在CSR-B中的相关操作进行PR值的更新（Line5~6），如果是减边操作则要扣除之前多加上的值，而如果是加边操作则要加上对应的值。当某轮PR值与上一轮的差值小于设定阈值时结束迭代。

算法3-2 链表方法calPR

输入：CSR-A,CSR-B

输出： PageRank Value in the target time

1. initialize:float array PR[]

2. for i=0 up to max_interation do

3. change = 0

4. for node in nodes do

5. accumulate rank in CSR-A

6. update rank according to ope in CSR-B

7. rank += damping_value

8. change += |PR[node] - rank|

9. update PR[node] with rank

10. end for

11. if change < threshold then

12. break

13. end if

14.end for

15.return PR

5.3 Parallel Method

维护一个邻居集合来表示某个点出现过的邻居，同时维持一个bitset<query_count>结构来表示每个目标时间该邻居是否存在，所以如果需要表示所有边，就需要一个长度为边长，元素为bitset的数组bitset<query_count> nei_exist[edge_count]。假若在第二个目标时间中，CSR结构中边数组的第index个边存在，那么nei_exist[index][1] = 1，反之则为0。同时维护两个二维数组node_exist,以此来记录每个目标时刻中节点存在状态和出度的信息。比如在第二个目标时间中这样扫一遍数据之后就知道所有的信息。不同的计算模块凭借时间去遍历每个点的所有出现过的邻居，看看该时间对应的标志位上是否为1，为1表示该邻居该时刻存在，否则不存在。然后就可以计算每个点的PageRank值，以此达到并行的效果。

在算法4-1中，如果目标时间都集中在前半部分，那么我们只需读snapshot数据，否则我们需要读取全部数据(Line2~5)，这些文档都按照被指向节点排序过。之后根据存在v中的Δ数据来更新nei_exist，同时逐步建立CSR结构(Line7~12)。之后根据每个target time与nei_exist中相应的状态进行PageRank并行计算(Line13)。

算法4-1 并行法PageRank

输入：Historical graph data v[4],target time array t[]

输出： PageRank Value in every target time

1. initialize:bitset array nei_exist[]

2. if last target time < half_time then

3. read front part of the historical file

4. else

5. read whole part of the historical file

6. end if

7. while True do

8. reload v

9. node2,node1,ope,time←v[0],v[1],v[2],v[3]

10. update nei_exist

11. Build CSR

12.end while

13.calPR(nei_exist,all target time) in Parallel way

5.4 算法总结

Serial Method中使用的CSR结构则是利用两个数组来实现的，数组的物理存储是连续的，空间占用也较链表来得小，但是我们需要给出数组的长度，以至于其不会浪费空间也不会造成溢出。访问数组中的数据会快于链表。在整合构建CSR前需要对已有数据进行排序，时间复杂度为O(nlogn),之后计算PageRank值时访问数据只需要在CSR中访问即可，时间复杂度为O(1)。

Parallel Method中仅需要扫描一遍按时间及被指向结点排好序的数据，之后按照操作类型填入该边该时刻是否存在即可，该步骤时间复杂度为O(n)，a代表每个点平均。在计算某时刻PageRank值时候访问CSR结构，获取数据的时间复杂度都为O(1)，即可计算。

6 实验

6.1 实验设置

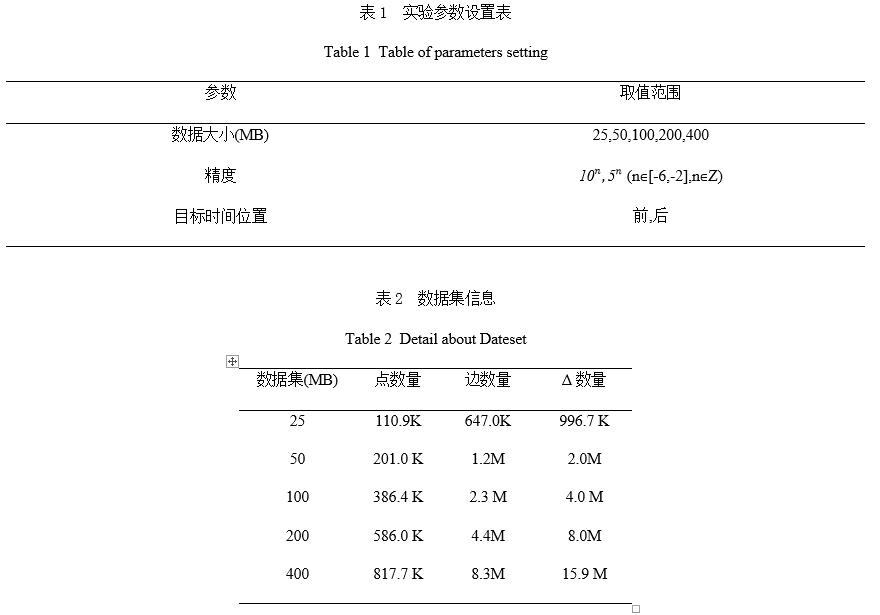
实验数据来自KONECT，内容纪录的是网页互相连接的Hyperlink networks，实验中不同大小的数据集都源自该数据集。

数据集中每行数据都是一个四元组(v1,v2,+/-,t)，表示在t时间增加或者删除v1指向v2的边。

表1展示了实验参数的设置，表2展示了每个数据集的特征。

实验在以下环境进行：

CPU：16 Intel(R) Xeon(R) CPU E5-2620 v4 @ 2.10GHz，总核数：8

内存：231022144 kB，约220GB

操作系统：Linux

6.2 实验1：PageRank迭代轮次实验

6.2.1 实验说明

我们知道PageRank值需要通过多次迭代才能达到收敛，我们意在探寻不同大小的图的收敛轮次之间存在的一些关系以及同一个数据集迭代的轮次和计算收敛的阈值之间的变换关系。

我们对于每个数据集，控制其计算阈值，记录不同阈值下的迭代轮次，以阈值为横轴，迭代轮次为纵轴作图。实验结果如图3-1所示。

6.2.2 实验分析

从图中可以看出，随着阈值的增大，迭代轮次全部表现为下降趋势，即阈值越小，所需迭代轮次越大；阈值越大，所需迭代轮次越小。

另外，普遍来说，数据集越大，对于相同的阈值所需的迭代次数越大，但是也存在不同数据集在相同阈值下迭代轮次相同或者小的数据集迭代轮次大于大的数据集的情况。

我们可以得出普遍的结论：阈值越大，数据集越大，所需的迭代轮次也就越大。

6.3 实验2：多参数的性能测试

6.3.1 实验说明

实验测试上述三个方法随着查询量增大而发生的改变。其中可变的参数包含查询位置、查询跨度。查询位置的前后分别代表着查询集中在时间轴的前半部分和后半部分，这样表示两种情况，分别是查询均匀分布在时间轴前半部分和后半部分。

6.3.2 实验数据图

6.3.3 实验分析

由图3-2可以看出一般来说计算的查询时间集中在后半部分的时候计算时间会比集中在前半部分的多，因为需要读取snapshot数据的原因。

另外，无论数据大小、查询位置是什么参数，计算时间会随着问询量的增大而增大，而且，根据图中的线条来看，查询时间和查询的数量是呈线性关系。

整体来看，使用其他两个使用CSR结构的方法会比使用链表的来得快些。其中LinkedList Method大大快于链表，而Parallel Method在准备数据过程中可能有所耗时，但是后续计算可以并行进行，也会对效率有所提高。

6.4 实验3：单次问询性能测试

6.4.1 实验说明

之前的测试是在不同跨度，不同问询量的情况下进行测试的。而我们测试的时间是诸多个问询量总共的计算时间，我们也只能得到计算每个问询的平均时间，而无法获知这些在时间戳轴上不同位置的问询所需时间的不同。

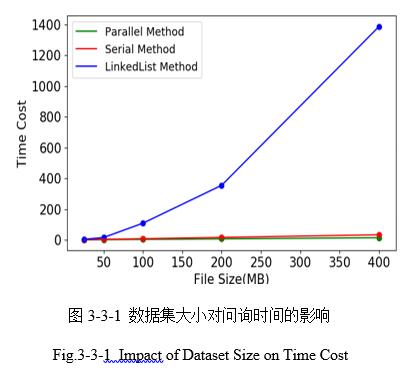
为了更加直观的获知数据集大小和查询时间的关系，我们针对不同数据集，只问询其最大时间戳处的PageRank值，以此来获得他们之间的关系。实验结果如图3-3-1所示。

另外，为了探究整个过程的时间主要耗费在什么地方，实验统计了三个方法在不同数据集下准备数据时间与总时间的比（总时间包括准备数据时间和计算时间）。实验详情如图3-3-2所示。

6.4.2 实验分析

从实验图3-3-1中可以看出随着数据集的不断增大，使用链表来解决问题的时间将会急剧增加，而使用CSR结构来解决问题的Serial Method、Parallel Method则表现出平稳的态势，二者性能大大优于使用链表的方法。

从实验图3-3-2中可以看出，链表方法的大部分时间都花费在准备数据上，也就是对图结构的维护操作中。在准备数据上，LinkedList Method花费了总时间的90%左右，而Serial Method也花费了75%左右，Parallel Method花费40%左右。由此我们可以得出，计算部分的时间并不是总耗时的决定因素，如何能高效地维护更新数据才是提高效率的关键。

结束语

本文在历史图的数据上进行PageRank问题的相关计算，介绍了历史图的基本特征和PageRank的基本思路。在研究主要解决思路时，考虑到历史图的各种性质（如频繁增删）和处理效率，若使用链表结构，在数据量庞大的情况下其查询所耗费的时间将会很大，因此我们使用CSR结构作为主要的数据结构。在此基础上借鉴串行计算和并行计算的思想产生了两个不同的方法，并分析了他们各自的特点。

实验表明，使用CSR结构解决历史图上PageRank问题的性能确实会优于使用链表结构，而且效果明显。

目前，在单机情况下，对于处理多个问询Parallel Method的效率低于Serial Method的效率。在接下来的工作中会考虑使用分布式数据处理系统来对Parallel Method进行实验优化，尝试提高其计算效率。

参考文献

[1]WU J P,LIN S,XU K,et al.Advances in Evolvable New Generation Internet Architecture[J].Chinese Journal of Computer,2012,35(06):1094-1108.

吴建平,林嵩,徐恪等.可演进的新一代互联网体系结构研究进展[J].计算机学报,2012,35(06):1094-1108.

[2]Przytycka T M, Singh M , Slonim D K.Toward the dynamic interactome:It's about time[J].Briefings in Bioinformatics,2010,11(1):15–29.

[3]CAO J.Analysis of Google's PageRank techno-

logy[J].Journal of Information,2002(10):15-18.

曹军.Google的PageRank技术剖析[J].情报杂志2002(10):15-18.

[4]Chang J W,DAI D H.Personalized Recommend-

ation Algorithm Based on PageRank and Spectral Method[J].Computer Science,2018,45(S2):398-401.

常家伟,戴牡红.基于PageRank和谱方法的个性化推荐算法[J].计算机科学,2018,45(S2):398-401.

[5]LI C S,LIU X G,JIAO H T et al.An Improved PageRank Algorithm Based on APP Search System[J].Computer and Modernization, 2018(07):24-27+38.

李春生,刘小刚,焦海涛,张可佳.基于APP搜索系统的PageRank改进算法[J].计算机与现代化,2018(07):24-27+38.

[6]Francisco Pedroche,Esther García,Miguel Romance,et al.On the spectrum of two-layer approach and Multiplex PageRank[J]. Journal of Computational and Applied Mathematics,2018,344.

[7]Harary F,Gupta G.Dynamic graph models[J]. Mathematical and Computer Modelling, 1997, 25(7):79-87.

[8]DING L L,LI Z D,JI W T, et al.Reachability Query of Large Scale Dynamic Graph Based on Improved Huffman Coding[J]. Acta Electronica Sinica,2017,45(02):359-367.

丁琳琳,李正道,纪婉婷,宋宝燕.基于改进哈夫曼编码的大规模动态图可达查询方法[J].电子学报2017,45(02):359-367.

[9]WANG C,CHEN L.Continuous Subgraph Pattern Search over Graph Streams[C]// International Conference on Data Engineering. IEEE, 2009.

[10] FAN W , LI J , LUO J , et al.Incremental graph pattern matching[C]//Acm Sigmod International Conference on Management of Data. ACM, 2011.

[11]Choudhury S, Holder L, Chin G, et al.Proc. of the Workshop on Dynamic Networks Management and Mining[C]// International Conference on Management of Data. SIGMOD/PODS'13, 2013.

[12]WU L K,XIAO X K,DENG D X, et al.Shortest Path and Distance Queries on Road Networks:An Experimental Evaluation[J].Proceeding of the VLDB Endowment, 2012,5(5):406-417.

[13] Page L,Brin S,Motwani R,et al. The PageRank Citation Ranking: Bringing Order to the Web[J]. Stanford Digital Libraries Working Paper,1998, 9(1):1-14.

[14]WEI Z W,HE X D,X X K,et al. TopPPR: Top-k Personalized PageRank Queries with Precision Guarantees on Large Graphs[C].// International Conference on Management of Data.SIGMOD,2018.

[15]HAVELIWALA,T.H .Topic-sensitive pagerank: A context-sensitive ranking algorithm for web search[J]. IEEE Transactions on Knowledge and Data Engineering, 2003, 15(4):784-796.

[16] ROUL R.K., SAHOO J.K., ARORA K. Query-Optimized PageRank: A Novel Approach[M]. Computational Intelligence in Data Mining. Advances in Intelligent Systems and Computing. Singapore:Springer,2019:673-683

[17]LI C C,KANG Z J,YU H G, et al. Identification Method of Key Nodes in Power System Based on Improved PageRank Algorithm[J]. Transactions of China Electrotechnical Society,2019,34(09):168-175.

李昌超, 康忠健, 于洪国, et al. 基于PageRank改进算法的电力系统关键节点识别[J].电工技术学报, 2019, 34(09):168-175.

[18]LIU Z Y,LI Q F,CENG C, et al.An Optimization Method of PageRank Based on Spark and its Application Research[J].Journal of CAEIT, 2018(4):399-405.

刘振宇, 李钦富, 曾操, et al.基于Spark的PageRank算法优化及其军事应用研究[J]. 中国电子科学研究院学报, 2018(4):399-405 

分享让更多人看到