4 Hardness Analysis And Heuristic Algorithms

Although we use the topology structure to reduce the problem's complexity, it is still difficult to solve the problem within a reasonable time. Thus, we reduce the problem's complexity by taking into account two real constraints to convert the problem into two general sub-problems: the Max-NCA problem, which aims to maximize the NCA improvement with a given upgrading cost, and the Min-Cost problem, whose objective is to deploy the minimum number of SDN switches to achieve the maximum NCA improvement in a network. In this section, we first prove the hardness of the two problems and then propose a heuristic algorithm to solve the two problems..

4.1 Max-NCA problem and its hardness

The Max-NCA problem is to maximize the NCA improvement under the constraint that the upgrading cost is less than or equal to a given upgrading budget:

Theorem 1: The Max-NCA problem is an NP-hard problem.

Proof: First, we can convert the Max-NCA problem to a Weighted Set Cover problem.

In the Weighted Set Cover problem, there is a link-set E with n elements: . Link-set E can be decomposed into m subsets: , and the subsets are associated with their weights . We treat the flow set F as the set of E, and each node in the network as the subset $S_i$. Of course, the flows passing through node $v_i$ correspond to the elements of the subset , the cost of the switch corresponds to the weight of the respective subset . By construction, it is easy to verify that there exists the maximum number of flows controlled under the budget, if and only if there exists the optimal solution to the Weighted Set Cover problem under the resource constraints.

The construction can be done in polynomial time and the Weighted Set Cover is an NP-hard problem [22]. Hence, the Max-NCA problem is also NP-hard.

4.2 Min-Cost problem and its hardness

The objective of the Min-Cost problem is to deploy the minimum number of SDN switches to control all flows in a network.

Theorem 2: The Min-Cost problem is NP-hard.

Proof: We can convert the Min-Cost problem to the Minimum Weighted Vertex Cover problem.

Given an example of the Minimum Weighted Vertex Cover problem. It includes the point set N, which has k elementsand the link set E which has m elementsthe points have corresponding weightAll points and links form a graph. We treat the flow set F as the link set E, and each nodein the network as the pointin the graph. Of course, the flows go through node corresponding to the links connected to pointthe cost of each switch corresponding to the weight of the point. Through construction, it is easy to prove that there exists the minimum cost to deploy SDN switch to control all the flows, if and only if there exists the optimal solution to the Minimum Weighted Vertex Cover problem.

The construction can be done in polynomial time and the Minimum Weighted Vertex Cover is an NP-hard problem [22]. Hence, the Min-Cost problem is also NP-hard.

4.3 Heuristic algorithm

We propose a heuristic algorithm for the Max-NCA and the Min-Cost problems. It greedily selects SDN switch to deploy based on the flows and the cost of the switch. The algorithm can effectively solve the above two issues within a short time.

In Algorithm 1, the inputs are the network G = (V,E), the budgetand the flow-set F. The output of the algorithm is the set of selected SDN switches.

Line 4 guarantees that the cost of the deployment is under budget or the set of flows is not empty. In line 5 of the algorithm, it greedily selects the optimal node to deploy on the basis of the flows and the cost of the node. For the Max-NCA problem, it adds the value of the selected node toin line 7 of the algorithm. For the problem Min-Cost, F subtracts the flows of the selected node in line 11 of the algorithm. The selected nodes are added to the set of Q in line 8 and 12. We assume the number of switches in the topology is $m$, and it deploys at most k SDN switches under budget. For the Max-NCA problem, the time complexity of the algorithm is O(km). We assume the number of flows in the topology is n. For the Min-Cost problem, the time complexity of the algorithm is O(mn).

5 Simulation

In this section, we evaluate our solution against the baseline scheme in real network topologies. Since the flows between node pairs are dynamically generated, and the size of each flow is also dynamic, we use the average control flow number as the experimental parameter [23]. We use $\sigma$ to indicate the percentage of the controlled flows.

5.1 Comparison schemes

We propose the algorithm 1 to solve the problem that incremental deployment SDN switches in hybrid networks. The simulation results of the following algorithms are compared with each other to evaluate the algorithm 1.

Heuristic: The scheme uses Algorithm 1 to update nodes to SDN switches.

Degree-first: The scheme in [15], they choose the next switch $u$ to upgrade by computing the maximum number of links incident to the SDN switch.

Random: The scheme randomly selects nodes to upgrade to SDN switches in the network.

Near-optimal: It is a brute-force scheme that obtains the near-optimal solution by enumeration. To reduce the complexity of the original problem, it involves some techniques, which selects the special nodes to upgrade to SDN switches. The details are shown in Section III.D.

5.2 Simulation setup

In our simulation, we use two real network topologies the ISP 1755 with 322 nodes and the ISP 3967 with 539 nodes from the Rocketfuel [10][24]. In real networks, there may be no communication between some node pairs. Thus, we consider two cases. In Case 1, each node transmits flows to all other nodes, while in Case 2, only a part of node pairs communicate with each other. The path of each flow is calculated using the OSPF protocol. However, we can only get network topologies and infer the link weights of each edge form Rocketfuel [24]. Therefore, the traffic matrix of the large network topology can only be generated randomly according to the link weights of each side.

5.3 Simulation results

Case 1: flows between all nodes.

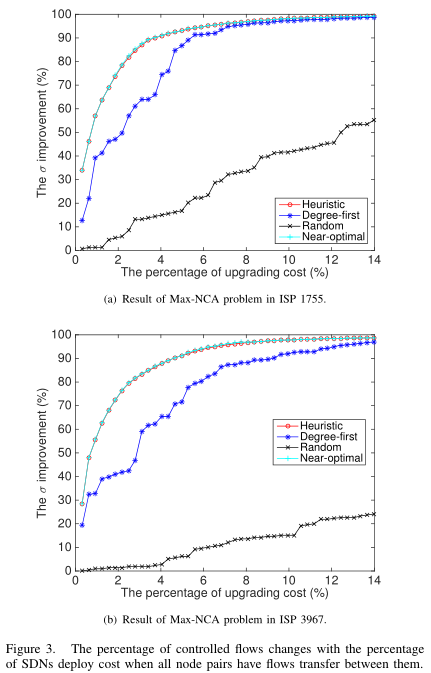
Fig.3 shows the results of the problem Max-NCA in ISP 1755 and ISP 3967. Among the three schemes, Random performs the worst. In Fig.31, Random requires 14% cost to improve 55% of $\sigma$, while Heuristic needs only 2\% cost. Heuristic needs only 10% cost to realize 98% of $\sigma$ improvement. The advantage of the heuristic is obviously better than the Degree-first when the percentage of upgrading cost is less than 8\% in Fig. 31 or less than 14% in Fig. 32. The performance of the heuristic algorithm is comparable to Near-optimal algorithm because it first chooses the core node with maximum flow to update.

Table 2 and table 3 show theimprovement in the ISP 1755 and the ISP 3967. Seen from Fig. 32 and Table 3, the results of Heuristic outperform Random and perform very close to Near-optimal. Comparing Fig. 31 with Fig. 32, we can conclude that with the extending of the network scale, Heuristic's advantage is more apparent than Random.

Case 2: flows between certain node pairs.

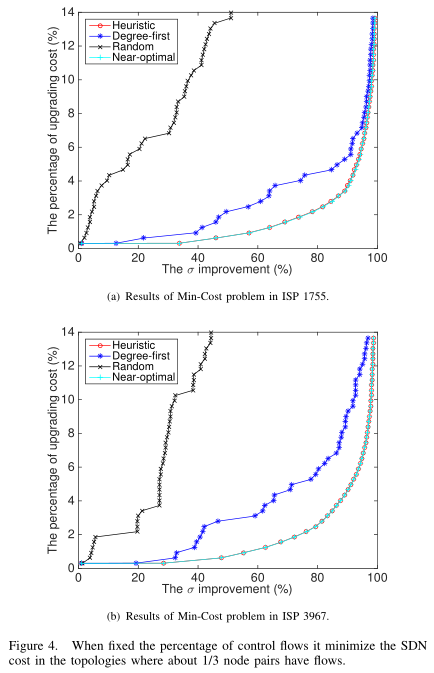
We compare these results in two instances that 1/3 node pairs have flows to transmit in Fig. Fig.4, and 2/3 node pairs have flows to transmit in Fig. 5. For the two cases, we randomly generate node pairs 100 times and ran our algorithms 100 times to get the average value on a high-performance computer. In the real network, the flows are dynamically generated, so the average value of 100 experiments is realistic and persuasive.

From Fig. 4, we can see the minimum percentage of SDN switch cost when fixed the proportion of the control flows.

The Fig.4 shows that, when we want to control 95\% of the number of flows, we need to upgrade only about 6\% of the nodes to SDN switches. Similar to the results of Fig.3, the Heuristic algorithm in Fig.4 also outperform Degree-first algorithm and perform very close to the Near-optimal algorithm. Compared Fig. 4 to Fig.5, the heuristic algorithm can achieve good results whether 1/3 node pairs have flows or 2/3 node pairs have flows.

In addition, the Fig.4 and Fig.5 show that the results of the algorithms are similar even in different topologies. Moreover, the Heuristic is always better than Degree-first in any case. Therefore, our algorithms are universal and extensive.

Table 4 and 5 show the upgrading cost of Heuristic and Near-optimal algorithms when fixing the $\sigma$ in the two topologies.

Since following the heavy-tailed distribution, the percentage of upgrading cost is relatively large when $\sigma$ is equal to 100\%.

6 Conclusions and Further Work

In this paper, we propose a scheme to deploy SDN switches incrementally in hybrid SDNs. Taking into account the real constraints, we propose two general problems: the Max-NCA problem and the Min-Cost problem. The hardness of the two problems are proved. Then we propose a heuristic algorithm for the two sub-problems. The heuristic scheme has low complexity and can intelligently select a few nodes to upgrade to SDN switches. The simulation shows that our scheme can achieve 95% of the number of flows controlled with only about 10 % upgrading cost. In the next work, we will try to improve the quality of service (QoS) through packet classification and flow scheduling based on the controllable flows.

References

[1] S. Agarwal, M. Kodialam, and T. Lakshman, “Traffic engi-neering in software defined networks,” in Proceedings of IEEEINFOCOM.IEEE, 2013, pp. 2211–2219.

[2] S. Jain, A. Kumar, S. Mandal, J. Ong, L. Poutievski, A. Singh,S. Venkata, and Wanderer, “B4: Experience with a globally-deployed software defined wan,” in Proceedings of ACM SIG-

COMM.ACM, 2013, pp. 3–14.

[3] M. Gholami and B. Akbari, “Congestion control in softwaredefined data center networks through flow rerouting,” in Elec-trical Engineering (ICEE), 2015 23rd Iranian Conference on.

IEEE, 2015, pp. 654–657.

[4] P. Lin, J. Bi, and H. Hu, “Btsdn: Bgp-based transition for theexisting networks to sdn,” in Ubiquitous and Future Networks(ICUFN), 2014 Sixth International Conf on.IEEE, 2014, pp.419–424

[5] A. Basta, W. Kellerer, M. Hoffmann, K. Hoffmann, and E.-D. Schmidt, “A virtual sdn-enabled lte epc architecture: a casestudy for s-/p-gateways functions,” in Future Networks andServices (SDN4FNS), 2013 IEEE SDN for.IEEE, 2013, pp.1–7.

[6] C. Filsfils, N. K. Nainar, C. Pignataro, J. C. Cardona, andP. Francois, “The segment routing architecture,” in in proceed-ings of the Global Communications Conference (GLOBECOM).

IEEE, 2015, pp. 1–6.

[7] S. Vissicchio, L. Vanbever, and O. Bonaventure, “Opportunitiesand research challenges of hybrid software defined networks,”ACM SIGCOMM Computer Communication Review, vol. 44,no. 2, pp. 70–75, 2014.

[8] Y. Guo, Z. Wang, X. Yin, X. Shi, J. Wu, and H. Zhang,“Incremental deployment for traffic engineering in hybridsdn network,” in Computing and Communications Conference

(IPCCC).IEEE, 2015, pp. 1–8.

[9] C.-Y. Chu, K. Xi, M. Luo, and H. J. Chao, “Congestion-awaresingle link failure recovery in hybrid sdn networks,” in Com-puter Communications (INFOCOM), 2015 IEEE Conference on.

IEEE, 2015, pp. 1086–1094.

[10] N. Spring, R. Mahajan, and D. Wetherall, “Measuring isptopologies with rocketfuel,” in ACM SIGCOMM ComputerCommunication Review, vol. 32, no. 4.ACM, 2002, pp. 133–145.

[11] Z. Li, Q. Li, L. Zhao, and H. Xiong, “Openflow channeldeployment algorithm for software-defined afdx,” in DigitalAvionics Systems Conference (DASC), 2014 IEEE/AIAA 33rd.IEEE, 2014, pp. 4A6–1.

[12] Y. Guo, Z. Wang, X. Yin, X. Shi, and J. Wu, “Traffic engineeringin sdn/ospf hybrid network,” in Network Protocols (ICNP), 2014IEEE 22nd International Conference on. IEEE, 2014, pp. 563–568.

[13] D. Levin, M. Canini, and Schmid., “Panopticon: Reaping thebenefits of incremental sdn deployment in enterprise networks,”in Proceedings of USENIX ATC 14, 2014, pp. 333–345.

[14] N. McKeown, T. Anderson, H. Balakrishnan, G. Parulkar,L. Peterson, J. Rexford, S. Shenker, and J. Turner, “Openflow:enabling innovation in campus networks,” ACM SIGCOMMComputer Communication Review, no. 2, pp. 69–74, 2008.

[15] D. Levin, M. Canini, S. Schmid, and A. Feldmann, Panopticon:Reaping the benefits of partial sdn deployment in enterprisenetworks. Die Professoren der Fakult?t IV, Elektrotechnik undInformatik, 2013.

[16] Z. Ying, C. Zhang, and Y. Wang, “Social based throwbox place-ment in large-scale throwbox-assisted delay tolerant networks,”in Communications (ICC), 2014 IEEE International Conferenceon.IEEE, 2014, pp. 2472–2477.

[17] G. Carrozzo, R. Monno, B. Belter, R. Krzywania, K. Pentik-ousis, M. Broadbent, T. Kudoh, A. Takefusa, A. Vieo-Oton,C. Fernandez et al., “Large-scale sdn experiments in federatedenvironments,” in Smart Communications in Network Technolo-gies (SaCoNeT), 2014 International Conference on.IEEE,2014, pp. 1–6.

[18] J.-L. Chen, Y.-W. Ma, H.-Y. Kuo, and W.-C. Hung, “Enterprisevisor: A software-defined enterprise network resource manage-ment engine,” in System Integration (SII), 2014 IEEE/SICEInternational Symposium on.IEEE, 2014, pp. 381–384.

[19]“Theswitchesofofficial\quoted.”[Online].\Available:http://product.yesky.com/switchboard/list2.html

[20] M. Carrión and J. M. Arroyo, “A computationally efficientmixed-integer linear formulation for the thermal unit commit-ment problem,” Power Systems, IEEE Transactions on, vol. 21,no. 3, pp. 1371–1378, 2006.

[21] B. Fortz and M. Thorup, “Internet traffic engineering by opti-mizing ospf weights,” in INFOCOM 2000. Nineteenth annualjoint conference of the IEEE computer and communicationssocieties. Proceedings.IEEE, 2000, pp. 519–528.

[22] T. H. Cormen, Introduction to algorithms.MIT press, 2009.

[23] S. Azodolmolky, P. Wieder, and R. Yahyapour, “Performanceevaluation of a scalable software-defined networking deploy-ment,” in Software Defined Networks (EWSDN), 2013 SecondEuropean Workshop on.IEEE, 2013, pp. 68–74.

[24]“Therouter-levelispropologiesfromrocketfuelproject:.”[Online].Available:http://research.cs.washington.edu/networking/rocketfuel/. 

分享让更多人看到