摘要

随着大数据的发展，大规模的数据越来越多的以密文的形式存储在云服务器中。本文重点讨论了在云服务器中，如何对已加密的数据进行快速的范围搜索。当可信任的数据持有者将加密的数据上传到云服务器后，云服务器支持大量的用户搜索数据，并在不可解密数据及查找范围的前提下，对数据搜索进行精确的匹配。本文提出了通过建立安全索引的方式对一维、二维数据进行范围查询的模型，并用百万的数据验证了方法的可行性与正确性。

关键词 隐私保护 范围查询 HMAC加密 数据索引

ABSTRACT

With the vigorous development and progress of big data, cloud server plays an important role in the data storage and processing.The paper focuses on fast range query based on the encrypted data . When trusted data owner upload the encrypted data to the cloud server, a large amount of users can search data from cloud server. The cloud server should accurately match the data range and return to the users .This paper established a fast range model based on encrypted data. With one million Twitter site data experimental verification, we prove that our model is feasible and efficiency.

KEY WORDS Privacy-Preserving Range Query HMAC Data Index

第一章 绪论

1.1 研究背景

为了数据运行的高可靠性、高运算性能和快速的计算能力，人们越来越多的利用云服务器来运行数据以及计算服务。而在云计算中，隐私问题成为关键。

云计算模型中涉及三个实体，数据持有者和客户都是可信任的，云服务器是不可信任的，因此数据持有者和客户的数据以及查询范围都以密文的形式发送给云服务器。

1.2 研究意义

当前的云服务器不支持加密数据搜索，如果解决了云服务器中加密数据搜索问题将会极大的改善数据安全问题并可应用于许多实际场景中，因此这个研究问题是非常重要也是今后必须解决的问题。而当前的方法[1,2,3,4]都不足以保护隐私并且高效的搜索，本文提出的算法将把隐私保护与快速搜索相结合，提出一种新的范围搜索模型。

1.3 主要贡献

本文主要做出如下贡献：

1．在已有一维数据搜索模型基础上提出了新的二维数据搜索模型。

2．对二维搜索模型做出了创新型的优化，使搜索效率有了明显提高。

3．提出了将二维搜索模型应用到KNN[5,6]（K邻近点搜索）等实际应用场景中，解决了实际的搜索问题。

1.4 搜索模型系统架构

对于一维数据和二维数据，我们都采用如图1-1所示的搜索模型，这个模型由Alex最先提出[7]。

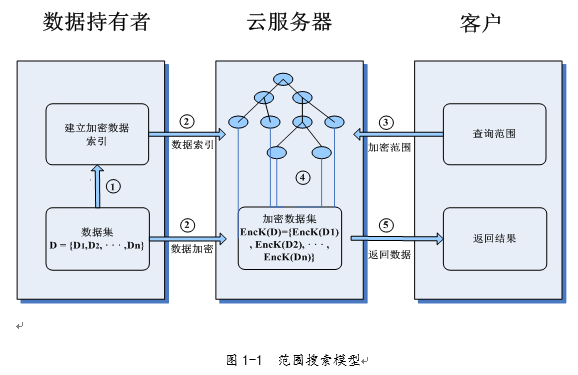
工作流程已在图中标明：

①由数据持有者利用原始数据集建立一个加密数据索引。

②数据持有者用对称密钥K对原始数据集进行加密，得到加密数据集，并将加密数据集以及上一步得到的数据索引上传给云服务器。

③客户端将查找范围进行HMAC加密后上传给云服务器。

④云服务利用加密数据索引对搜索范围进行查找。

⑤云服务器将查询到的加密数据返回给客户，客户利用对称密钥K对加密数据进行解密，得到原始数据。

第二章 一维数据搜索模型

对应于上一章的系统架构，本章对一维数据搜索[7]主要从数据持有者建立数据索引，客户端上传搜索范围，云服务器进行范围查询这三个方面进行讨论。

2.1 数据持有者建立数据索引

建立数据索引主要包括三个步骤：

1.进行前缀编码：将原始数据表示成二进制形式，并用这个而二进行所有的前缀组成前缀编码集合。

2.建立平衡二叉树的数据索引：将上一步中的前缀编码建立一棵平衡二叉树，建树方式与数据大小顺序无关，从而保证索引结构不可分辨性。

3.进行HMAC加密[8]并映射到Bloom Filter[9]：对于上一步中建立的平衡二叉树内的元素（数据的前缀编码）进行HMAC加密。对于根节点，使用H个不同密钥对原始数据进行加密，并且在树的每一层引入一个v.R的随机数进行二次加密，从而消除节点间相同元素的相关性。并将加密的值映射到一个Bloom Filter的位数组中，从而减小数据索引的空间大小。

2.2 客户端上传搜索范围

客户采用与数据持有者相同的前缀编码方法对数据范围进行前缀编码，将查询范围转化为最小的前缀编码集S(a,b)，使这个集合的前缀数最少，且可以表示这个范围。将S(a,b)同样用与数据持有者相同的密钥进行H次HMAC加密，将加密的数据集上传给云服务器。

2.3 云服务器进行范围查询

对于客户端传来的加密搜索范围，云服务器将每一个加密数据与树型索引的每一个节点进行Bloom Filter的匹配，若匹配则可判断该节点下的叶子节点中存在满足范围的数据，则继续遍历此子树直到遍历到叶子节点，云服务器将叶子节点指向的数据传给客户端，完成搜索过程。

第三章 二维数据搜索模型

不同于一维数据的前缀编码，对于二维数据本文采用栅格编码对数据进行转换。

3.1 数据持有者建立数据索引

二维模型中建立数据索引也需要三个步骤：

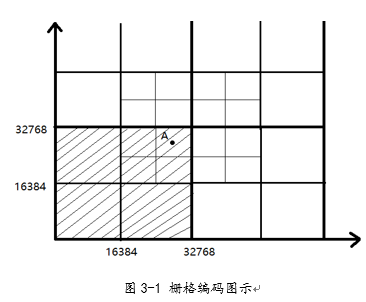
1.栅格编码[10]：

对于二维数据，本文将二维数据映射到一个平面，并对这个平面进行栅格的划分，如图3-1。将每一个点用K级的栅格编码进行表示（本文对于栅格采用格子中心点坐标来表示此格子的编码），即完成栅格编码。

2.建立平衡四叉树的数据索引,由于在二维平面中利用栅格划分，每一级栅格都将平面分为四个部分，因此我们采用平衡四叉树来存储数据的索引。建立方法与一维模型中方法相同。

3.将上一步的数据索引进行HMAC加密并映射到Bloom Filter 中，具体方法与一维搜索模型方法相同。

3.2 客户端上传搜索范围

与一维数据不同，二维数据（如地理位置）搜索上传的范围一般是以客户端所在的地理位置为圆心，以r为搜索半径的一个圆形搜索范围，如图3-2。在客户端同样采用栅格编码的方法，将这个二维平面进行栅格的划分。这个圆形的搜索范围将包含如图中填色的这些栅格。用这些栅格来表示客户的搜索范围。

下一步，对圆形搜索范围所覆盖的栅格编码进行HMAC加密，并将加密的数据上传给云服务器。

3.3 云服务器进行范围查询

云服务器对二维数据搜索过程与一维模型介绍方法基本相同，此处不做赘述。

3.4 二维数据搜索的优化

本文采用栅格编码的方法已将搜索范围转化为一个简单高效的表示方法，为了提高搜索速率，我们需要从数据索引的结构进行讨论与优化。本章中通过优化数据索引的结构（广度优化）以及搜索过程（深度优化）从而提高搜索的速率。

广度优化指将相邻的点尽量分配到数据索引的同一棵子树中，这样可以减少查询次数。但为了数据安全，设置阈值T，当一个节点内数据个数大于T时，才可进行广度优化。

深度优化是指，当一个节点内元素全部满足范围时，则直接返回其子树的所有叶子结点。这就需要建立数据索引时，保存每个节点内的公共栅格编码，从而使查询时减少查询的深度。

第四章 实验验证

4.1 实验数据集

本文从推特网站上收集了一百万个用户的位置数据，数据包含用户的ID，用户位置的x坐标与y坐标。坐标以经度和纬度的格式存储。我们分别进行三个实验，实验一是用二维搜索模型进行二维数据范围的搜索，实验二是采用优化的二维搜索模型对二位数据范围进行搜索，实验三是采用Alex提出的一维搜索模型进行二维数据范围的搜索，并记录每个实验中数据索引的建立时间，数据索引的空间大小，范围搜索的时间，范围搜索的结果误差等，并通过实验间的对比来分析不同模型的优缺点。

4.2 实验结果分析

4.2.1 搜索时间分析

在三组实验参数设置相同的情况下，通过改变搜索范围进行多次实验，实验结果都标明，利用优化的二维搜索模型进行搜索的效率大大高于其他两组对比实验，而一维搜索模型的实验中搜索时间是最长的。

对于实验二，保证其他参数不变，改变安全阈值T，当T值越大时，代表优化程度越低，实验中搜索时间越长，当T大于总数据个数时，代表未进行优化，则实验二搜索时间与实验一相同。

4.2.2 数据索引建立时间分析

实验中，通过记录数据索引的建立时间可知，优化的二维搜索模型的数据索引建立时间远大于其他两个实验组的数据索引建立时间，其他两个实验组建立时间相近，对于一百万的数据，优化的二维搜索模型大约需要建立7000s，而其他两个实验组建立大约3000s。

4.2.3 搜索误差分析

本文提到过，当对二维搜索范围进行栅格编码时，我们存储的栅格是搜索范围完全覆盖的栅格，因此对于覆盖一部分的栅格被我们忽略，这就产生了搜索结果的误差。本文拿实验一进行实验，通过改变栅格级数来计算误差。实验结果标明，栅格级数越大，误差越小，当栅格级数为15级时，误差为百分之三。

第五章 结束语

本文在已提出的一维模型基础上设计了针对二维数据范围的搜索模型，使二维的加密数据可以以很高的效率进行搜索，并且同时保证了数据的安全性。在二维数据范围搜索模型的基础上，本文又对二维数据同时进行了深度优化以及广度优化，将搜索速率大大的降低。

对于二维加密数据的搜索，在现实生活中也有很多应用的场景，如KNN搜索问题等，因此本文讨论的问题具有很多实际的应用价值。

参考文献

[1] B. Hore, S. Mehrotra, M. Canim, and M. Kantarcioglu. Secure multidimensional range queries over outsourced data. The VLDB Journal, 21(3):333–358, June 2012.

[2] B. Hore, S. Mehrotra, and G. Tsudik. A privacy-preserving index for range queries. In VLDB, pages 720–731, 2004.

[3] A. Boldyreva, N. Chenette, Y. Lee, and A. O’Neill. Order-preserving symmetric encryption. In EUROCRYPT, pages 224–241, 2009.

[4] A. Boldyreva, N. Chenette, and A. O’Neill. Order-preserving encryption revisited: Improved security analysis and alternative solutions. In CRYPTO, 2011.

[5] N. Li, T. Li, and S. Venkatasubramanian. t-closeness: Privacy beyond k-anonymity and l-diversity. In Data Engineering, 2007. ICDE 2007. IEEE 23rd International Conference on, pages 106–115, April 2007.

[6] W. K. Wong, D. W.-L. Cheung, B. Kao, and N. Mamoulis. Secure knn computation on encrypted databases. In SIGMOD, pages 139–152, July 2009.

[7]Rui Li, Alex X. Liu, Ann L. Wang, Bezawada Bruhadeshwar:Fast Range Query Processing with Strong Privacy Protection for Cloud Computing. PVLDB?7(14): 1953-1964(2014)

[8] Praveen Gauravaram, Shoichi Hirose, Suganya Annadurai.An Update on the Analysis and Design of NMAC and HMAC Functions.International Journal of Network Security, 2008, Vol.7 (1), pp.49.

[9] Kumar A,Xu J.Space-Code bloom filter for efficient per-flow traffic measurement. Proc.of the IEEE INFOCOM2004.

[10] Hien To, Gabriel Ghinita, Cyrus Shahabi:A Framework for Protecting Worker Location Privacy in Spatial Crowdsourcing. PVLDB?7(10): 919-930 (2014). 

分享让更多人看到