摘 要: 为了改善社交网络中影响最大化问题的算法的效率。我们针对社交网络中幂率分布的现象,提出了二分图模型。在模型中对影响的传播过程进行了限制，将社交网络划分为二分图，使得候选的种子集合大幅减小。此模型能够计算精确的影响力的同时避免了蒙特卡洛多次模拟，降低了复杂度。我们通过在一个真实数据集合上的测试,验证了二分图模型可以得到不错的结果。

关键词: 社交网络；影响最大化；幂率分布；二分图

引言

随着互联网的快速发展，网络空间出现了许多社交网络,譬如腾讯QQ，Facebook，新浪微博等等。不同的社交网络由于拓扑结构不同而各有特点。在腾讯公司的即时通讯app微信中各个用户和好友关系组成的社交网络几乎不会有节点的度超过一万,并且每个节点和与其相连的大多数节点都是线下的朋友，联系紧密。IC模型最初就是用来在这样的社交网络上寻找有影响力的节点的。

但是随着新型社交网站的发展,出现了一些非传统的社交网络,这些社交网络在结构上与传统社交网络有很大不同。例如，在微博上的很多用户拥有上百万的粉丝量，而另一方面大量的用户的粉丝数目只有一百个左右。在youtube中一个视频会有百万次的点击率,另一方面大量的视频却无人问津。在这样的网络中之中,幂率分布(长尾效应)很明显,也就是说极少数个体对应极高的值，而拥有极低值的个体，数量却占总体的绝大多数。形象地描述可称曲线靠近纵轴的部份为tall head，而靠近横轴的部份则是所谓的long tail。如图1所示。

在幂率分布明显的社交网络之上解决影响最大化问题的话,根据经验,我们只需要在tall head之中选择我们需要的种子节点即可。 在此基础上我们对贪心算法进行了改进,通过对原始图形进行一些删减。并且在一个数据集合上进行了实验验证。证明了算法的高效。

本文主要贡献如下:(1)本文首次将幂率分布的特性应用到影响最大化问题之中进行问题求解。(2)本文对贪心算法进行改进得到了newgreedy算法,并且在幂率分布明显的图形上进行影响最大化问题的求解。(3)我们对贪心算法的改进和某些基于贪心算法的改进是兼容的。我们将celf算法的思想运用到了newgreedy算法得到了greedy++算法。

引言

Kempe, Kleinberg, and Tardos首先将这个问题形式化描述为离散最优化问题(Discrete Optimization Problem), 证明在常用随机级联模型(Stochastic Cascade Model)类的信息扩散模型 IC、LT 模型下求解影响力最大化问题最优解是一个 NP-hard 问题，然后给出了有证明保证(Provable Guarantee)的可求得 （1-1/e）≈63%最优的贪婪算法。但是 Kempe 所提出的近似算法十分耗时,在其论文的试验部分处理 15000 结点网络需要几天的时间,之后的研究主要关注于最优化近似算法的效率提高上。

针对这个问题，学界的工作大多是基于Kempe等人的工作，提出近似算法，改进算法的时间复杂度，或者提出新的扩散模型，在新的模型下进行研究算法，提升算法的可并行性，提高算法在大规模数据集合上的表现。

Leskovec 等人提出的改进方法 CEFL(Cost-Effective Lazy Forward)方法是一种新的使影响力最大的择初始结点优化方法，CELF 算法利用了 IC 模型的子模性(submodularity)，网络中加入一个结点到集合中得到的边际收益，要大于等于加入同一个结点到集合的父集所得到的边际收益。利用子模性大大减少了计算结点影响力传播效果的次数，减少选择初始有影响力结点的计算量。实验表明，CELF 算法结果接近贪心策略近似算法，但算法运算时间要快 700倍。在 CEFL 的基础上，Amit Goyal 等人利用子模性进一步优化了 CELF 算法，又提出了更高效的 CEFL++算法， 算法效率再次提高了 35-55%。

W．Chen 等主张启发式(heuristics)算法在影响最大化问题研究中的更优性，提出 Degree-discount 启发式算法，是目前基于理论扩散模型影响力最大化问题最高效的方法。

Degree Discount 算法思想：照度降序选择结点，每选中一个结点，将其邻居结点的度减小一个定值

正文

首先对“影响力最大化”给出形式化的定义：给一个有向图G = (V,E) ，V代表节点，E代表有向边，每一条边有一个权值pe ∈ [0,1]，代表源点对终点的影响因子(源点有多大的几率对终点产生影响)。定义参数向量θ=(pe ) e∈E 代表每一条边上的影响因子

我们定义σθ (S)为影响传播函数，（σθ (S)代表从S出发能传播到的所有节点数目的期望值）其中L代表图G的子图，Prθ [L]代表在参数向量θ下子图L出现的概率。（每一条边出现的概率就是传播因子）RL（S）代表在子图L中从S节点能到达所有节点的个数。

Influence maxization问题就是要找到使得σθ (S)取得最大值得集合。

在论文《基于目标话题的社会网络影响力最大化研究》之中,作者这样写道“人际关系中包括一些强联系(Strong tie)和弱联系(Weaktie)，区分这些连接的重要性在了解信息扩散机制十分重要。联系即网络中的边，联系的强弱反映到网络中即边权重值的大小，反映到信息扩散模型上，即不同边的信息传播概率或阈值的设置。在研究人员基于 Email 数据研究了用户之间的交互性对信息扩散的影响，发现信息从初始者到扩散者时通常会走弱关系边，而从扩散者到接收者时通常会走强关系边，说明信息在流动过程中有从弱关系到强关系的转向特征．另外发现扩散者并非中心性很强的社会化中心点(Social Hubs)，而是很普通的点，研究人员对比了所有用户的度分布和扩散者的度分布，发现非常匹配，证明了这个观点。 ” 通过对这段话的分析可以知道,我们在真实的影响传播途径之中,有着从弱关系到强关系的转向,现实之中大V节点对于普通人的影响力往往比较小,就是弱关系,而普通人之间的关系往往建立在物理世界的朋友关系即强关系,所以如果我们直接在大V节点之中选择种子节点,对于真实的影响传播过程影响不大。

针对影响最大化问题,在Influence Maximization Meets Efficiency and Effectiveness: A Hop-Based Approach这篇论文之中,作者提出了一个很有意思的思路,作者实验了影响力的传播随着传播跳数的增加而增加的情况,如图2所示。然后作者将跳数限制在了3步之内,去衡量种子节点集合的影响力,加速了影响力的计算过程。

这篇论文可以启发我们把影响力的传播进一步限定在一步之内。

图2展示了种子节点的影响力会随着影响传播过程的跳数增加而逐渐增加,并且传播一跳之后获得的影响力与不限制传播跳数获得的影响力之间存在近似常数的比值。所以我们将我们的影响力传播限制在了一跳。

我们的候选种子节点集合是整个社交网络图之中的大V节点构成的集合X,其余所有的节点构成集合Y,并且我们把影响力的传播限定在一步之内,那么我们得到的种子节点只能影响一部分X中的节点和Y中的节点,由于在幂率分布明显的图中,X集合相比Y小的多,这种情况下如果我们只考虑X中的种子节点对于Y中节点的影响,我们就会得到一个二分图。

由于二分图结构简单,我们可以使得我们的影响力计算问题复杂度成为线性, 在之前的影响最大化问题之中,影响力的计算是#p-hard的,我们只能采用蒙特卡洛算法,多次运行IC模型根据实际的结果得到种子节点集合的影响力。

在二分图中,种子节点集合影响力的计算就非常的简单,我们只需要计算Y中和受到种子节点影响的节点,计算他们受到影响的概率,然后相加。就得到了最终的影响力。

影响最大化问题的贪心算法伪代码:

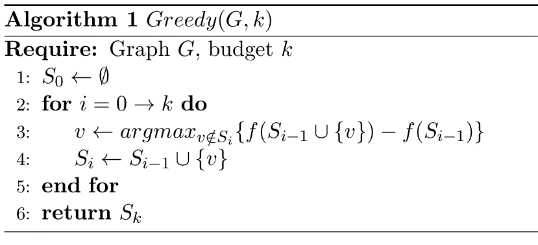
每一次迭代找到使得种子节点集合影响力增益值最大的节点,加入到种子节点集合之中。

由于二分图依旧是图,所以在二分图上的目标函数依旧满足

?非负性:f(S)>=0

?非递减性:f(S+v)\ge f(S)

?子模性: 记录N为所有的节点集合

所以我们可以将贪心算法应用到我们的二分图之中。

在二分图上算法NewGreedy和Greedy计算过程一样,但是影响力的计算变得简单了,并且种子节点的候选集合小了很多。由于我们的算法对于其他基于贪心算法的改进是兼容的,所以同时我们将CELF算法的思想应用到我们的NewGreedy算法之中,得到了我们的Greedy++算法。

1 复杂度分析

假设输入的二分图包含n个节点,m条边,其中集合A中节点数目是a,集合B中节点数目是b,种子节点个数是k。

Greedy算法要循环k次,每一次需要遍历所有节点,计算每一个节点的影响贡献值,计算一个集合的影响值需要运行r遍ic模型,将求得的影响值取均值以减小误差,运行一次的时间复杂度是m,综上时间复杂度是O(k*n*r*m)

NewGreedy同样需要循环k次,与Greedy所不同的是节点的选取只在集合A中,还有影响值的计算变的简单了,只需要计算一次时间复杂度是k*b,所以总的时间复杂度O(k*a*k*b)

"CELF是改进的贪心算法。会比传统贪心算法有近700倍的速度提升。" Greedy++是将CELF算法思想应用到NewGreedy之上,得到的改进算法。 Greedy++的时间复杂度上界也是O(k*a*k*b),但是实际情况下,算法相比Newgreedy算法会很快停止。 根据实际实验的结果平均时间复杂度是O(a*k*b)。

2 实验

我们首先需要得到网络的幂律分布情况。然后根据幂律分布的程度划分我们的种子节点候选集合X。然后将整个社交网络图划分成一个二分图,左边的节点是种子节点候选集合,右边的节点是其余的所有节点。然后在种子节点候选集合之中挑选种子节点,最后评价一下我们的算法和其他算法的优劣。

2.1 数据集介绍

我们斯坦福大学公布的一个数据集合上进行了实验,数据集合介绍和下载地址是https://snap.stanford.edu/data/ca-GrQc.html,这个数据集合是广义相对论和量子宇宙学协作网络,一共有 5242个节点14496条边。图3是我们在数据集合上进行的简单预处理,统计了节点的度。如图3所示,大尾效应还是比较明显的。

笔者在此数据集合上验证我们的算法。通过分析,我们将度最多的前两百个节点作为种子候选集合,并利用了图中节点的相似程度计算了节点之间的影响力。然后计算了四种算法,这四个算法分别是:greedy,degreediscount,newgreedy,greedy+。

2.2 参数设置

N(v) 定义为{u|(u,v)属于E} 表示对节点v有影响力的点。我们使用用户之间的关系作为参考来产生传播概率。 表示用户u对于用户v的影响力大小。 =(x*|N(u)∩N(v)|+1)/| N(v)|在上面的公式之中(|N(u)∩N(v)|)表示对于用户u和用户v共同朋友的个数。 x为人工设置的超参数。

我们将x设置成0.2。我们把图划分成了二分图,候选的种子节点集合大小是200，用来构造二分图。

2.3 结果分析

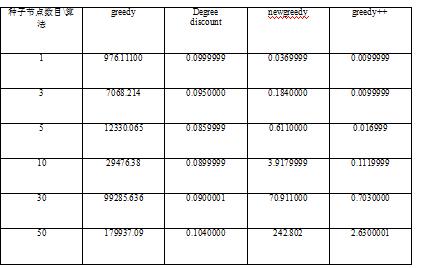
通过对表1的分析可以得知四种算法在理论上的时间复杂度确实在实验中得到了验正,在数据集合上, newgreedy对greedy进行了改进,时间复杂度具有数量级的优势, greedy++由于使用了CELF的思想所以进一步降低了时间复杂度，但是前面三个算法都比不上目前最快的算法degreediscount。不过degreediscount只是一个启发式的算法,并没有任何的理论保证。

表1 四种算法挑选不同数量种子节点的时间

传统算法之中由于节点集合的影响力评价采用了蒙特卡洛算法多次求解取平均值,所以对于贪心算法,计算的次数越多,结果越精确。但是时间随着计算次数增多线性增加。实验中我们迭代计算了100次，这也是贪心算法时间如此长的原因。

我们的算法由于部分采用了贪心算法,所以在二分图上运行的结果是和贪心算法一样有1-1/e的近似比，但是在原来的图中,并没有理论保证。

所以二分图能保留原来图中多少信息决定了我们的算法结果，这对我们候选集合的划分提出了挑战。

表2显示出我们的Greedy算法结果比较好. Degreediscount算法表现的并不稳定,这也符合之前的结论。接下来重点分析newgreedy和greedy++算法。我们的算法受到候选种子集合和与种子集合之间相对大小的影响，如果候选集合相比于我们的种子节点集合过小,那么我们在候选集合之中很难找到最好的种子集合,那么算法结果就不如我们的传统算法；如果二者相对大小合适,导致我们最优的种子节点组合出现在了种子候选集合之中,那么我们的算法的结果就会表现的很不错,不仅时间比贪心快了很多,而且甚至结果也可以超过贪心算法。这在表2中也得到了验证。

3 结论

我们在这篇论文之中, 将大尾效应应用到了影响最大化问题的求解之中,并且实验验证,取得了不错的实验结果。

分享让更多人看到