基于按需即时去扩展化的LTL公式到Büchi自动机直接转换算法研究

摘要：在显式状态模型检测技术领域，现实系统通常被表达成线性时序逻辑(LTL)公式，并被转换成Büchi自动机(BA)。为了提高转换的效率，当前很多转换工具使用了中间自动机，如扩展的Büchi自动机(GBA)。去扩展化就是将GBA转换成BA的过程。本文提出并实现了LTL公式到BA的直接转换算法。本文中首次提出使用一个新的标签---接受度(Acceptance Degree，)用于记录转换过程中状态和变迁上已经满足的接受条件。是给定的LTL公式中子公式的集合。根据，本文提出一种不同于经典去扩展化算法的方法---按需即时的去扩展化(On-the-fly De-generalization，)算法。算法在展开LTL公式的过程中根据需要执行，它不同于完全展开LTL公式后，再进行去扩展化的经典方法。利用算法，我们实现了LTL 公式到Büchi自动机的直接转换，不需要使用中间自动机保存转换过程中临时结果。通过使用五组常用的LTL公式和四组随机生成的LTL公式测试已有的转换工具和本文提出转换工具，实验结果显示本文提出的直接转换方法避免了传统转换算法中的多重转换步骤，降低了计算复杂度，所需的转换时间更短。

关键字：模型检测，LTL公式，Büchi自动机，接受度，按需即时去扩展化

 

1 引言

    模型检测[1，2]是一种能够对有限状态系统属性进行自动验证的技术。 如果给定一个有限状态系统和该系统需要满足的一系列属性，模型检测工具能够利用检测算法自动验证系统是否满足属性的要求。当前已有很多有效的模型检测算法，如符号化模型检测算法、显式状态模型检测算法等。在显式状态模型检测算法中，常用Kripke结构[3] M=(S，R，L)描述某个真实系统，利用图(graph)表述Kripke结构的有限状态模型，LTL公式描述系统需要满足的属性，这种方法称为LTL模型检测方法。LTL模型检测过程就是验证S中的所有状态是否满足，即

{ s ∈ S | M，s |= φ}

- S是一个有限的状态集合，

- R是状态间的变迁关系，

- L是状态的标记。

    LTL模型检测工具首先将LTL公式的否定范式转换为Büchi自动机(BA)，将该自动机与系统自动机进行笛卡尔积运算，然后检测乘积自动机是否存在反例。如果判空检测结果为空集，则系统满足属性的要求，否则存在反例，需要修改系统。LTL模型检测的过程如图1所示。表示待验证的LTL公式，sys表示待验证的系统模型，表示系统BA中的状态集合，表示状态间的变迁关系。检测sys是否满足的最差时间复杂度为，该时间复杂度与系统模型的大小成线性关系，而与LTL公式因子的数量成指数关系。由于LTL 模型检测是基于状态空间穷尽搜索算法，对于模型的每一个状态都要验证是否满足属性的要求。因此，使用更少的时间，生成更小的属性BA有助于改进模型检测的效率。

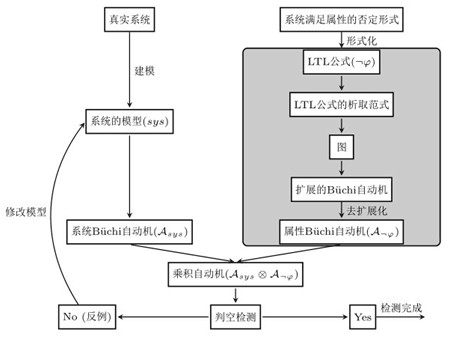
图1 LTL模型检测过程

    本文重点研究如何将LTL公式直接转换为BA，即LTL公式到BA的直接转换算法。在直接转换算法中，图1中阴影部分的中间自动机和中间步骤不再需要了，因此直接转换算法的转换效率更高。

    在LTL公式到BA的转换算法研究中，主要有两方面的研究工作。一种方法是基于tableau的构建方法，该方法使用GBA作为转换的中间自动机，对中间自动机进行去扩展化。在基于tableau的构建方法中，每一个状态上都标记了一个LTL子公式的集合，确保在一个可接受的运行(run)上所有的接受条件都将被满足，如Spot [5]，Spin [6]。另一种方法是先将LTL公式转换为交替自动机，在将交替自动机转换为扩展的Büchi自动机，最后进行去扩展化得到Büchi自动机，如LTL2BA [7]，LTL3BA [8]。

    Spot是基于tableau的构建方法的LTL模型检测算法的C++工具库。在Spot中，一种基于变迁的Büchi自动机(Transitions based Generalized Büchi Automata，TGBA)被用于中间自动机，TGBA被去扩展化为BA。R.Gerth等[9]提出了按需即时的基于tableau构建方法的LTL模型检测算法，将LTL公式转换为GBA，再将GBA去扩展化后得到BA。该算法已被应用于模型检测工具Spin。T.Babiak等[8]在LTL2BA的基础上提出一系列的改进方法，实现了一个新的转换工具LTL3BA。LTL3BA先将LTL公式转换为弱的交替自动机(Very Weak Alternating Automata，VWAA)，再将VWAA转换为TGBA，最后将TGBA去扩展化为BA。LTL3BA的时间复杂度为(是VWAA中状态的数量) [10]，这与基于tableau的构建方法的LTL模型检测算法的时间复杂度相同。

    [5，8，9]等方法都使用了中间自动机(如GBA或TGBA)。为了将GBA转换为BA，E. M. Clarke等在[4]的9.2.2节提出了GBA转换BA的经典算法。该算法也适用于将TGBA转换为BA [7，11]。一个具有个状态和个接受条件的GBA或TGBA，能转换成含有一个接受条件和最多个状态的等价的BA [12]。此外，A. Duret-Lutz[5]提出了一个更好的去扩展化算法，该算法按照固定的执行顺序将GBA去扩展化，执行顺序与对应的二叉决策图(Binary Decision Diagram，BDD)变量的存储顺序相同。T.Babiak等[13]提出基于最大强连通分量的去扩展化算法，该算法对经典的去扩展化算法做了部分改进，利用最大强连通分量的收缩性优化了算法效率。K.Chatterjee等[14]提出了去扩展化索引数的定义，该索引数应用于将Rabin扩展自动机去扩展化成Rabin自动机。

    本文提出了基于tableau的构建方法按需即时的LTL模型检测算法，能够实现LTL公式到BA的直接转换。根据自动机理论和LTL的语义，在LTL公式的扩展过程中就可以执行去扩展化。因为只有子公式需要去扩展化，通过跟踪自动机的每个状态和变迁上接受条件的满足情况，去扩展化过程可以在LTL公式展开的过程中根据需要执行。接受度(Acceptance Degree，)用于记录自动机上每个状态和变迁上的接受条件的满足情况。本文提出的直接转换算法与已有的算法[5，8，9]有以下两点区别：

    1.我们的转换算法能将LTL公式直接转换为BA，不再需要已有转换算法中的许多中间步骤和中间自动机。

    2. 按需即时的去扩展化(On-the-fly De-generalization，)算法在LTL公式展开的过程中根据需要执行，而在经典的去扩展化(Classic De-generalization，)算法中，去扩展化过程要在LTL公式完全展开后才能执行。

    本文的组织结构如下：第二节介绍了本文所需要的预备知识。第三节介绍了本文提出的算法的主要思想。第四节提出了LTL公式的BA的直接转换算法。第五节将我们的方法与已有的方法进行对比。第六节总结，提出下步工作。

 

2 预备知识

    在本节中，简介了线性时序逻辑和几种自动机的定义。

2.1 线性时序逻辑

    线性时序逻辑(Linear Temporal Logic，LTL)是用于描述未来的事情的时序逻辑。它将时间建模成无限长度的状态序列，该序列称为计算路径。LTL是描述一个系统的执行序列属性的语句，在形式化方法中常用于描述系统的约束条件。它包括许多操作符：

    -原子命题 (如：p，q，r等)，命题常量 ( T(True)，⊥(False))，

    -逻辑操作符 (? (not)，∧(and)，∨(or))，

    -时序操作符 ((neXt)，(Until)，(Release)，(Always)，(Eventually))。

    在线性时序逻辑中，原子命题是最常用的语句。若AP是原子命题的有限集合， 是一个原子命题，是AP的子集的集合，是由AP推导出的命题公式的集合。

    定义1 (LTL的语法) LTL公式的语法递归定义如下：

    - p，?p，T和⊥是LTL公式，

    - 如果φ和ψ分别是LTL公式，则?φ，，，，，，和是LTL公式。

    R公式是U公式的对偶式。依据如下恒等式，{R，F，G}公式能转换成U公式。

    - φ R ψ ≡ ?(?φ U ?ψ)

    - F φ ≡ T U φ

    - G φ ≡ ⊥ R φ ≡ ?F (?φ) ≡ ?(T U ?φ)

    根据如下恒等式，每个LTL公式都能写成等价的否定范式。

    - ?φ ∨ ?ψ ≡ ?(φ ∧ ψ) - ?φ ∧ ?ψ ≡ ?(φ ∨ ψ)

    - φ ≡ ?(?φ) - X ?φ ≡ ?(X φ) - G ?φ ≡ ?(F φ) - F ?φ ≡ ?(G φ)

    - ?φ U ?ψ ≡ ?(φ R ψ) - ?φ R ?ψ ≡ ?(φ U ψ)

    定义2 (LTL的语意) 若是一个字(word)，代表从字母开始的后缀序列，则满足关系 |= 定义如下:

    - ξ |= T

    - ξ |= p 当且仅当 p∈ξ[0]

    - ξ|= ?φ 当且仅当 ?(ξ |= φ)

    - ξ |=φ∧ψ 当且仅当 ξ |=φ 且 ξ |=ψ

    - ξ |=φ∨ψ 当且仅当 ξ |=φ 或 ξ |=ψ

    - ξ|=X φ 当且仅当 ξ1 |= φ

    - ξ|=F φ 当且仅当 存在i ≥ 0，ξi |= φ

    - ξ|=G φ 当且仅当 对于任意i ≥ 0，ξi |= φ

    - ξ|= φ U ψ 当且仅当 存在j ≥ 0，ξj |= ψ，且对于任意0 ≤ i < j，ξi |= φ

    - ξ|= φ R ψ 当且仅当 存在j ≥ 0，ξj |= φ，且对于任意0 ≤ i < j，ξi |= ψ；或 对于任意k ≥ 0，ξk |= ψ

2.2 自动机

     前一小节介绍了LTL的语法和语义。LTL模型检测是基于有限自动机是否满足无限字的验证过程，因此我们简要介绍一下有限状态自动机的定义。有限状态自动机是具有固定的内存和相互独立输入系统的数学模型，它包括有限输入字的有限状态自动机和无限输入字的有限状态自动机(也称为ω自动机[ ω自动机是具有无限输入的有限状态自动机的变种，常用于表达不期望中断的系统的特殊行为。]) 两种。最简单的无限输入的自动机是Büchi自动机。

    定义3 (Büchi自动机) Büchi自动机(BA)是一种接受条件标注在状态上的ω自动机，也称为基于状态的Büchi自动机。一个非确定的BA的形式化定义为一个五元组

    - 是有限的状态集合，

    - 是输入字母的有限集合，也称为的字母表，，

    - 是一个非确定的变迁函数，每一个变迁上都标注了变迁条件，

    - 是初始状态的集合，

    - 是接受状态的集合。

    当且仅当，且时，是确定的Büchi自动机。

    若是无限输入字。自动机的运行(run) ?是在上的序列，是初始状态，当i≥0时，。 若表示在上无限出现的状态集合，当且仅当时，在无限字上的运行被自动机接受，也就是说，当某些接受的状态在运行无限出现时，被自动机接受。当无限字ξ有一个接受的运行时，被接受。

    定义4 (扩展的Büchi自动机) 扩展Büchi自动机(Generalize Büchi Automata，GBA)的定义与BA相似，不同点是GBA有多个接受条件的集合。GBA形式化定义为一个五元组

    - Q是有限的状态集合，

    - Σ是输入字母的有限集合，也称为的字母表，Σ=2AP，

    - : Q × Σ → 2Q是一个函数，称为的变迁函数，

    - 是初始状态的集合，

    - 是接受状态的子集的有限集合，。

    当满足时，GBA就变成BA。当且仅当时，在无限字ξ上的运行被接受，即在上无限出现的状态集合中至少包含中每个集合中的一个状态时，被自动机接受。

    定义5 (基于变迁的扩展的Büchi自动机) 接受条件标注在变迁上的GBA被称为基于变迁的扩展的Büchi自动机(TGBA)。TGBA形式化定义为一个五元组

    - 是有限的状态集合，

    - 是输入字母的有限集合，也称为的字母表，，

    - 是一个变迁关系，每一个变迁上标注一个布尔公式和一个接受条件的集合，

    - 是初始状态的集合，

    - 是接受变迁的子集的有限集合，。

    若是一个无限字。在上的运行是一个序列，，， q_1)。若表示在无限出现的变迁的集合，当且仅当, 时，被接受。当在无限字上的运行被接受，则被接受。

    定义6 (接受条件) 接受条件(Acceptance Condition)是字[字是无限长的字]的无限集合。在无限运行的系统中，我们关心的是一个特定的动作是否无限多次的重复出现。如果在一个运行上接受条件无限多次出现，该运行就是期望的无限多次出现的动作。下面是几种不同的接受条件：

    - BA的接受条件

    当且仅当时，BA接受运行。是BA的接受条件，虽然是一个有限集合，但它等价于 (是自然数)被接受的条件。

    - GBA的接受条件

    当且仅当时，GBA接受运行，等价于被接受的条件。

    - TGBA的接受条件

    当且仅当时，TGBA接受运行，等价于被接受的条件。

    虽然接受条件是字的无限集合，为了方便研究，接受条件通常看作有限的表示。自动机的接受条件由给定的LTL公式的子公式组成，子公式可以表示无限的序列，同时接受条件包含空集。

 

3 GBA到BA去扩展化的改进方法

    本节将详细介绍GBA到BA去扩展化算法的改进方法，下一节将介绍LTL公式到BA的直接转换算法。

    3.1 tableau构建方法

    在定理证明中，tableau构建方法(也称为真理树)用于对语句和相关逻辑的决策，是一阶逻辑的证明过程[15]，也用于对不同逻辑公式集合的满足性进行判断，是模态逻辑最常用的证明过程[16]。tableau构建方法通过证明逻辑公式的否定范式的不满足性论证逻辑公式成立。tableau构建方法往往从一个主连接词开始，利用一系列的规则依次展开逻辑连接词，在多数情况下是将逻辑公式一分为二。

    LTL公式的tableau构建方法用于将LTL公式展开成一个图，它把LTL公式的时序逻辑连接词分成两部分，一部分是当前状态下已经得到满足的子公式，另一部分是在下一状态要满足的子公式。在一个状态上标记的公式完全展开后，才对下一个状态上标记的公式进行处理。LTL公式的tableau构建方法展开的图通常是树，树的唯一根节点是给定的公式。树的孩子是根据表1中的规则依次展开对应的子公式。当没有规则可以应用时，则到达树的叶子结点。叶子结点只能包含原子命题及其否定形式、命题常量等。

表1 LTL公式的tableau构建规则

    LTL公式的tableau构建过程如下：首先，将给定的LTL公式改写成等价的否定范式，并定义为初始状态的标签。然后利用Tableau规则递归展开，直到没有子公式出现在公式的顶层，结果公式的析取范式重写成一个覆盖 (cover)。为了分离当前已经满足的部分和下一状态满足的部分，在每一个状态上分别标记已经满足的公式。cover的每一个析取项表示在状态上标记的子公式，命题文字表示在当前状态已经满足的子公式，部分表示在下一状态需要满足的子公式。命题文字也是当前状态出边的标记，部分表示本状态出边的后继状态。例如，公式(1)表示和展开过程，在的cover中有两个命题文字和一个子公式。

    (1)通过观察展开过程，我们发现 (i) 成立，立即得到满足；(ii) 成立，将在下一状态继续验证，直到被满足。如果被验证无限次而始终没有满足，(ii)式是一个无限序列。扩展过程与相似。同理，和也会产生无限序列。

    虽然LTL公式的tableau构建过程能很好的展开LTL公式，一个重要问题是如何判断一个无限序列是我们想要的接受运行。对于BA的无限长度的运行，只要接受条件无限多次出现在该运行时，它就是我们想要的接受运行。

3.2 接受度

    为了跟踪哪些接受条件在自动机的每个状态和变迁上得到了满足，本文提出一个新标签---接受度()。是在每一个状态和变迁上已经得到满足的接受条件的集合。根据，我们能确定哪些接受条件在当前的状态和变迁上得到了满足。

    定义6 (接受度) 接受度(Acceptance Degree，)是在每一个状态和变迁上已经得到满足的接受条件的集合，标记在每一个状态和变迁上。

    - ，是状态数，是变迁数，

    - ， 是在每一个状态和变迁上已经满足的接受条件，。

    函数用于表示，它是接受条件集合到自动机的每一个状态和变迁的映射关系。(是初始状态)。若(resp.)代表第i个变迁(resp.状态)上得接受条件。 和根据下面的规则进行定义:

    - 是第i个状态，是第i个变迁。是的出边。是的标签。

    - 表示自状态开始的序列需要满足的接受条件。

    -的定义如下: 若是一个LTL公式，

    是自动机的一个运行， 。 如果|=， 且 ，那么。

    例如，我们利用LTL公式的tableau构建过程将转换为自动机，公式扩展过程如图2所示。有两个接受条件，分别用白点和黑点(○，●)表示。图2中的两个自动机都是利用Tableau规则展开的。图2(a)所示的是与一致TGBA，图2(b)所示的是附加了 (在花括号中)的自动机。根据，我们可以知道在每个状态和变迁上哪些接受条件得到了满足。如果在一个运行上，所有的接受条件被满足了无限多次，则该运行时接受的运行。

图2 的扩展过程。(a)与相对应的TGBA。 (b)与相一致的并附加了的自动机

3.3 去扩展化

    在很多转换工具中，LTL公式被转换为GBA或TGBA，但在很多情况下，LTL公式被转换为只有一个接受条件的BA更便于处理。去扩展化就是将GBA转换成BA的过程。

3.3.1 经典的去扩展化方法

    GBA 的接受条件为。使用经典去扩展化方法将该GBA去扩展化成BA的过程如下所示:

    首先, 我们构建去扩展化自动机

    - 是一个有限状态集合，是原自动机被复制m+1层，

    - 是输入字母表的有限集合，

    - 是初始状态集合，即在第一层的初始状态，

    - 是接受状态的集合，即最后一层的接受状态的集合，

    - 是一个变迁关系。，y根据下面的规则进行定义：

    然后，去扩展化自动机需要精简。在去扩展化自动机中最多有个状态，但是很多状态时无效的。无效的状态和变迁需要删除，等价的状态和变迁需要合并。以第一层初始状态为起点，满足每一个接受条件集合中的至少一个接受条件，并且到达最后一层的满足状态的运行是接受的运行。这种构建方法确保在去扩展化自动机中的接受运行与GBA中无限的多次经过所有接受条件的运行相对应。例如，利用算法去扩展化与相一致的的TGBA的过程如图３所示。有两个接受条件，分别用黑点和白点(●，○)标记。在图３中，在每层的状态上标记的数字表示该状态所在的层号。在去扩展化自动机中，除了第一层，每一层的状态至少满足一个接受条件，最后一层满足所有的接受条件。在去扩展化自动机中，所有变迁根据每一个状态上的接受条件加入自动机，即满足的变迁将连接到满足的下一个状态。

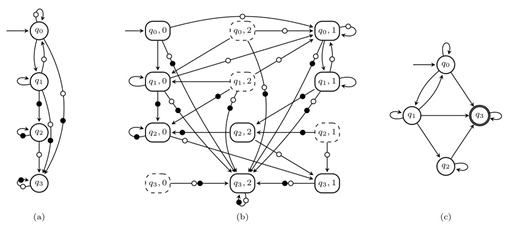
图3 利用算法去扩展化与相对应的TGBA(为了便于阐述，变迁上的标签被删除)。　(a)与相对应的TGBA。 　(b)与TGBA相一致的去扩展化自动机，虚线部分是无效的状态。 　(c)与相对应的BA。

3.3.2 按需即时的去扩展化方法

    在算法中，原自动机被复制了层，根据在每一层的状态满足的接受条件将变迁加入的去扩展化自动机中，有可能的接受条件的排列顺序和个初始状态的选择方法，因此，在去扩展化自动机中总共有个可能的去扩展化路径。为了避免这些组合的可能性，我们提出了改进的去扩展化的方法：按需即时的去扩展化算法。

    算法的思想如下：在扩展LTL公式的过程中，每一个状态和变迁上已经满足的接受条件被附加到这些状态和变迁上，用于记录已经满足的接受条件。根据状态和变迁上的，变迁被加入到自动机中。变迁的等于该变迁的目的状态的，即如果，变迁就连接到状态上。事实上，算法是在展开LTL公式的过程中执行去扩展化。在状态上附加的接受条件等同于在算法中的每一层满足的接受条件，根据在状态和变迁上满足的接受条件把变迁加入到自动机中。在算法中，不需要构建去扩展化自动机，LTL公式可以直接转换成BA。

    在图４中，利用算法直接将公式转换成BA。有两个接受条件。根据Tableau规则递归展开，由于记录已经满足的接受条件并被附加的状态和变迁上。的计算过程是递归的，即下一个是根据当前的计算的。变迁被加入到自动机中，满足的变迁连接到满足的下一个状态，即满足●的变迁连接到满足●的下一个状态。如果一个状态满足所有的接受条件，这个状态就是BA的终态。这就确保了BA中的接受运行满足所有的接受条件。

图4 利用算法将直接转换成BA，用黑点和白点(●，○)标记。　(a)在状态和变迁上附加了，并与相一致的图。　　(b)与相一致的BA。

    与经典的算法相比，按需即时的去扩展化算法运行的效率更高，因为在展开LTL公式的过程中不需要构建中间自动机，用于构建去扩展化自动机和移除冗余状态和变迁的时间可以节省下来。我们使用算法实现了LTL公式到BA的直接转换算法。

 

4 LTL公式到BA的直接转换算法

    当前，已有很多先进的算法用于将LTL公式转换成BA，这些算法可分为图５所示的四个步骤。

    step 1: 重写LTL规则。应用LTL恒等式重写LTL规则，移除冗余部分，使得公式更适合于高效的转换。

    step 2: 根据LTL公式构建图。根据Tableau规则，将LTL公式转换成图。

    step 3: 精简图，将图转换成中间自动机(GBA或TGBA)。

    step 4: 去扩展化。将中间自动机去扩展化成BA。

图5 LTL公式到BA的转换步骤，虚线部分表示本文中对转换算法的改进方法

    我们对每一步进行独立处理，重点关注第二到第四步。在第二步，递归计算，并将附加到状态和变迁上。第三步和第四步合并，第二步生成的图直接转换成BA. 根据上面提出的思路，我们设计并实现了一个新的转换工具TUAD，TUAD的主算法如算法１所示，部分变量定义如下所示：

    - NodeSet：未处理的状态集合，

    - DisjunctSet：cover}的析取项的集合，

    - q，q'：q代表当前状态，q'表示q的下一个状态，

    - 、：自动机的变迁，

    - l： 状态和变迁上的标签。

    算法１实现了直接将LTL公式转换成BA。算法的思想如下：根据Tableau规则展开公式，并构建图，是图的根节点，对应于自动机的初始状态的标签。在展开公式的过程中使用深度优先搜索算法，记录展开公式的析取范式。对于每一个析取项，利用算法2和3计算状态和变迁上的，并将附加的对应的状态和变迁上。如果新状态在图中不存在，则该状态直接加入到图中，否则丢弃。根据算法将变迁加入到图中，如果图中没有变迁，则直接加入图；如果图中已经存在变迁与的原状态、目的状态相同，则将和合并成新的变迁，变迁的合并过程包括标签合并和合并，即， 。如果在一个状态上，所有的接受条件都得到了满足，该状态就是接受状态。最终，将图转换成BA。

    算法１中最耗时的部分是计算LTL公式的 cover的过程。在本文工作中，在公式展开的每一步我们移去了冗余的状态和变迁，构建的中间自动机更小。算法有助于减少图转换成BA的时间。虽然扩展算法的最差时间复杂度为，但在多次试验中未观测的最差时间复杂度的情况发生。

 

 

5 试验及结果比较

    在本节，我们测试TUAD、LTL3BA v1.0.2和SPOT v1.2.4三个转换工具，比较转换时间，生成自动机的状态数和变迁数。TUAD是利用C++语言开发的基于CUDD 2.5.0库[17,18]开发的转换工具，而SPOT 和LTL3BA 是基于BuDDy 库[19]开发的转换工具。TUAD应用算法，而SPOT和LTL3BA应用算法[5,8]。

   为了便于比较测试结果，我们在通用测试平台ltlcross [20]上使用以上3个转换工具对常用的5组LTL公式[21]进行测试，5组公式如下所示：

    同时，应用LTL随机生成工具LBTT 1.2.1[22]生成4组LTL公式对三个工具进行测试，比较测试结果。测试的硬件环境为：Pentium(R) Dual-Core CPU E5300 @2.6GHz，4GB内存。操作系统是Ubuntu 12.04 LTS。 为了比较测试结果，转换工具均生成的最简单公式形式。

    我们将5组常用公式的试验结果总结到附录A中的Table A1---A5中。n的取值范围是，运行时间限制在12小时内，如果在限制时间内没有响应，则标记N/A。为了直观的比较运行时间，我们将三个转换工具的运行时间抽取出来以图的形式显示。

 

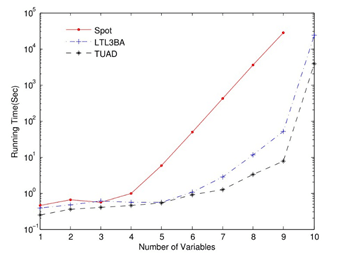
图6 将转换为BA所需时间对比图

    包含许多子公式。的最小BA有个状态。三个转换工具产生了相同数量的状态数。SPOT和TUAD应用了基于tableau构建的算法，但TUAD的运行时间明显少于SPOT；LTL3BA使用的转换算法不同于TUAD，但TUAD的运行时间少于LTL3BA。的运行时间比较如图6所示。

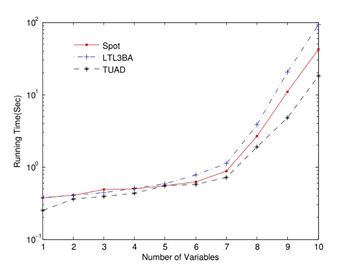
图7 将转换为BA所需时间对比图

    包含许多子公式。的最小BA包含个状态。 三个转换工具生成的BA的状态数和变迁数是相同的。TUAD的运行时间略快于其他两个工具。的运行时间比较如图7所示。

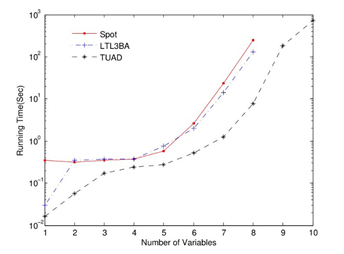
图8 将转换为BA所需时间对比图

    包含许多子公式。的最小BA包含个状态。三个转换工具生成的BA的状态数和变迁数是相同的。TUAD的运行时间略快于其他两个工具。运行时间比较如图8所示。

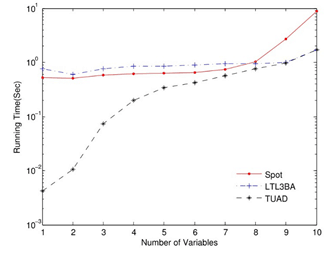
图9 将转换为BA所需时间对比图

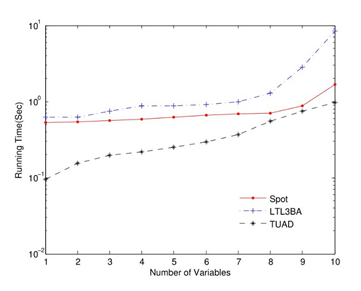
图10 将转换为BA所需时间对比图

    和包含许多子公式。和的最小BA包含个状态。三个转换工具生成的BA包含相同数量的状态，但变迁数是不同的。TUAD的运行时间快于其他两个工具。和的运行时间比较如图9-10所示。

     根据图6-10所示，对于5组常用的LTL公式，TUAD的运行时间少于SPOT和LTL3BA，说明本文提出的直接转换算法的运行效率比SPOT和LTL3BA高，按需即时的去扩展化算法的性能优于经典的去扩展化算法。　

    为了进一步比较测试结果，我们使用LBTT 1.2.1随机生成4组LTL公式，用以测试三个转换工具的性能。Benchmark1和Benchmark3包括300个长度为15-30的LTL公式及其否定形式，Benchmark1的原子命题数是3, Benchmark3 的原子命题数是8。Benchmark2和Benchmark4包含400个长度为25-40的LTL公式及其否定形式，Benchmark2的原子命题数是3, Benchmark4的原子命题数是8。LBTT的详细参数设置见附录A中的Table A6所示。

    Benchmark1-4的测试结果见表2所示。LTL公式是随机生成的，比较的公式的数量较大，测试对象覆盖了各种LTL公式。根据运行时间和生成BA的状态数和变迁数的累积结果可以看出TUAD的性能更优。

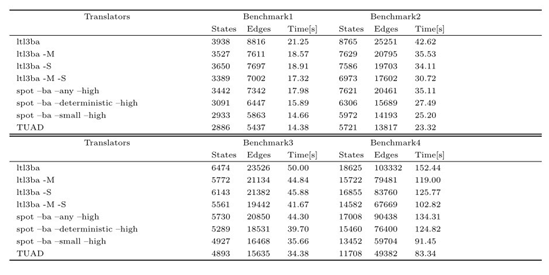
表2 利用Benchmark1-4测试转换工具累积结果对比

 

6 结束语

    在本文中，我们提出了基于tableau构建方法的LTL公式到BA的直接转换算法。和用来记录每一个状态和变迁上已经满足的接受条件，根据，我们提出了算法，并在直接转换算法中使用算法，试验结果表明LTL公式到BA的直接转换算法避免了传统转换算法中的多重转换步骤，以及对中间生成产物的化简操作，从而在很大程度上降低了计算复杂度，提高了转换效率。直接转换算法中对覆盖(cover)集合的计算带有一定的重复性，即如果已经计算过公式集合的覆盖，之后再次遇到集合时仍然会重新计算其覆盖。下一步我们将考虑对已计算的覆盖进行记录，使在此之后的重复计算只需要常数时间，进一步提高算法效率。

 

参考文献

[1]Clarke E M, Emerson E A. Design and synthesis of synchronization skeletons using branching time temporal logic. Springer Berlin Heidelberg, 1982.

[2]Queille J P, Sifakis J. Specification and verification of concurrent systems in CESAR. International Symposium on Programming. Springer Berlin Heidelberg, 1982: 337--351.

[3]Kripke S A. Semantical considerations on modal logic. Acta Philosophica Fennica, 1963, 16: 83--94.

[4]Clarke E M, Grumberg O, Peled D A. Model checking. the United States: MIT press, 1999

[5]Duret-Lutz A. LTL translation improvements in spot. In: The Fifth international conference on Verification and Evaluation of Computer and Communication Systems, British Computer Society. 2011, 72—83

[6]Holzmann G J. The model checker spin. IEEE Transactions on software engineering, 1997, 23(5): 279—295

[7]Gastin P, Oddoux D. Fast LTL to Büchi automata translation. In: Computer Aided Verification, Springer. 2001, 53—65

[8]Babiak T, K?etinsk? M, Rehak V, Strej?ek J. LTL to Büchi automata translation: Fast and more deterministic. In: Tools and Algorithms for the Construction and Analysis of Systems, Springer Berlin Heidelberg. 2012, 95—109

[9]Gerth R, Peled D, Vardi M Y, Wolper P. Simple on-the-fly automatic verification of linear temporal logic. In: Proceedings of the Fifteenth IFIP WG6. 1 International Symposium on Protocol Specification, Testing and Verification, IFIP. 1995, 253—271

[10]Boker U, Kupferman O, Rosenberg A. Alternation removal in Büchi automata. In: Automata, Languages and Programming, Springer. 2010, 76—87

[11]Giannakopoulou D, Lerda F. From states to transitions: Improving translation of LTL formulae to Büchi automata. In: Formal Techniques for Networked and Distributed Sytems - FORTE 2002, Springer. 2002, 308—326

[12]Renault E, Duret-Lutz A, Kordon F, Poitrenaud D. Three scc-based emptiness checks for generalized Büchi automata. In: Logic for Programming, Artificial Intelligence, and Reasoning, Springer. 2013, 668—682

[13]Babiak T, Badie T, Duret-Lutz A, K?etinsk? M, Strej?ek J. Compositional approach to suspension and other improvements to LTL translation. In: Model Checking Software, Springer. 2013, 81—98

[14]Chatterjee K, Gaiser A, K?etinsk? J. Automata with generalized rabin pairs for probabilistic model checking and LTL synthesis. In: Computer Aided Verification, Springer. 2013, 559—575

[15]Wolper P. The tableau method for temporal logic: An overview. Logique Et Analyse, 1985, 28(110–111): 119–136

[16]Girle R. Modal logics and Philosophy[M]. McGill-Queen's Press-MQUP, 2000.

[17]Somenzi F. Cudd: Cu decision diagram package-release 2.4. 0. University of Colorado at Boulder, 2009

[18]Somenzi F. Cudd: Cu decision diagram package, release 2.5. 0, 2012. Software available from http://vlsi. colorado. Edu

[19]Lind-Nielsen J. Buddy: A binary decision diagram package. Technical report, 1999

[20]Duret-Lutz A. Manipulating LTL formulas using spot 1.0. In: Automated Technology for Verification and Analysis, Springer. 2013, 442–445

[21]Cichon J, Czubak A, Jasinski A. Minimal Büchi automata for certain classes of ltl formulas. In: Dependability of Computer Systems, 2009. DepCos-RELCOMEX’09. Fourth International Conference on, IEEE. 2009, 17–24

[22]Tauriainen H, Heljanko K. Testing LTL formula translation into Büchi automata. International Journal on Software Tools for Technology Transfer, 2002, 4(1): 57–70